最近老是想起陈芝麻烂谷子的事情,说明工龄所剩无几了。
- 1 -又是在那遥远的 2009 年,那个“杯具”已经不是杯具的年头,度厂办个算法比赛,办出了点儿杯具的味道。
比赛的名字叫“百度之星”,那些年在校园里影响力还蛮大的(好像现在还是),大概赛制就是通过初赛、复赛、决赛这么几轮,选出几个社会主义四有青年
瓜分奖金。值得一提的是,头两年(05、06)冠军都被楼教主承包了。
为什么说有点杯具的味道呢,因为那年的初赛结束以后,度厂搞了个骚操作,把所有参赛选手提交的代码导出来,打了个包,发在贴吧里。
于是贴吧突然就炸了。
 - 2 -
- 2 -要知道初赛是网络赛,各个学校的 ACM(或OI) 集训队的队员们很可能都是凑在机房一起参与,毕竟毛主席教导我们人多力量大嘛。

所以这就有点意思了:如果同一个题,两份代码长得很像,说明互相抄袭概率就很大。
问题是参赛人数有点多,两两对比这 O(n^2) 的时间复杂度,靠人肉有点儿吃不消;但这么大一个瓜,光看不吃又有点可惜了。
那么这瓜到底该怎么吃呢?
- 3 -还好,作为一个竞赛战五渣的我,通过初赛的能力没有,搞事情的能力还是有一点的。

为了对比两份代码的相似度,那我首先得找到一个指标。
作为一个善于
作弊 思考的社会主义三无青年,我估计作弊者在拿到弊友代码后不会直接提交,至少会做些更换变量名之类操作;但竞赛时间紧迫,大概率来不及修改整体框架。
那么,只要我能算出修改的程度,就能判断相似度了:假设两份代码长度分别是 m、n,修改了 x 个字符, 我们大致可以把 `100% - x / ((m + n) / 2)` 当成相似度(没被修改的字符占比)。
但如何计算这修改的程度呢?毕竟修改前后代码长度很可能不同,不适合通过逐字比较来找到差别。
- 4 -既然直接处理两段代码有点棘手,那不妨先考虑一下简单的 case 。
比如说要将字符串 "a" 改成 "b",这个简单,只要改一个字符就行。
又比如说要将字符串 "a" 改成 "ab",这个也简单,只要添加一个字符就行。
再比如说要将字符串 "ab" 改成 "b",这个依然简单,只要删除一个字符就行。
如果我能算出将一段字符串通过添加、删除、修改三种操作修改成另一个字符串的
最少操作次数,应该就能把这瓜给吃了。

好像是找到了方向,但是要怎么实现呢?
- 5 -既然直接处理两段代码还是有点棘手,那不妨再考虑一下稍微复杂一点的 case ,比如把字符串 X = "baidu" 变成 Y = "bytedance"。
首先,因为 X[0] 和 Y[0] 相同,我们可以把问题简化成:将 "aidu" 变成 "ytedance",即 X[1..4] => Y[1..8](后面简记为 X[1:] => Y[1:])。
接着,X[1] = 'a', Y[1] = 'y',如上一节所说,这时候我们有三种选择:
*
添加:给 X 添加 'y' ,当成 "byaidu",于是问题简化为将 "aidu" 变成 "tedance",即 X[1:] => Y[2:];(注意,我们在这里把该操作当成一个思维实验就好,不需要真的修改 X ,所以这里 "aidu" 对应 X[1:] 而不是 X[2:])
*
删除:从 X 中删掉 'a' ,当成 "bidu",问题简化为将 "idu" 变成 ytedance",即 X[2:] => Y[1:];
*
修改:把 X 这个 'a' 改成 'y',当成 '"byidu",问题简化为将 "idu" 变成 "tedance",即 X[2:] => Y[2:];
这三种操作中,后续需要的修改次数最少的那个,再加上 1,就是我们把 X[1:] 改成 Y[1:] 所需的最少次数。
依此类推,如果我们将 X[i:] 变成 Y[j:] 需要 f(i, j) 次操作,由上可得到这样一个公式:
if X[i] == Y[j]:
f(i, j) = f(i + 1, j + 1)
else:
f(i, j) = 1 + min(
f(i, j + 1), #添加
f(i + 1, j), #删除
f(i + 1, j + 1) #修改
)
也就是说,我们可以用子问题的最优解来推导出问题的最优解,如果用不说人话的方式,就叫做该问题存在
最优子结构。
这么一看,代码是不是呼之欲出了?
- 6 -啰嗦了这么多,不能忘了大佬的教导:

说干就干,把上面推导的公式落地成代码,so easy:
def change(x, y):
def f(i, j):
if x[i] == y[j]:
return f(i + 1, j + 1)
else:
return 1 + min(
f(i, j + 1),
f(i + 1, j),
f(i + 1, j + 1)
)
return f(0, 0)
print change("baidu", "bytedance")
然后跑起来一看:
$ python change.py
Traceback (most recent call last):
File "change.py", line 13, in <module>
print change("baidu", "bytedance")
... #省略一大段
File "change.py", line 3, in f
if x[i] == y[j]:
IndexError: string index out of range
 - 7 -
- 7 -"index out of range",越界了 —— 显然,这里漏掉了递归的终止条件。
不过这个简单:如果 X 越界了,说明这时 i == len(X),那么 Y 还剩几个字符,我们都加上就行,即还需要 len(Y) - j 次操作;或者 Y 越界了,说明 j == len(Y),我们把 X 剩下的几个字符删掉,即 len(X) - i 次操作。
于是代码变成了:
def change(x, y):
def f(i, j):
if i == len(x):
return len(y) - j
if j == len(y):
return len(x) - i
if x[i] == y[j]:
return f(i + 1, j + 1)
else:
return 1 + min(
f(i, j + 1),
f(i + 1, j),
f(i + 1, j + 1)
)
return f(0, 0)
print change("baidu", "bytedance")
跑起来效果杠杠的,马上就得到了 7,算得没毛病。
只可惜这代码还没法用 —— 别说跑那些参赛代码,就连长度为 16 的两个字符串都跑不出结果……
- 8 -稍微分析一下我们就会发现,它竟然是指数时间复杂度的:
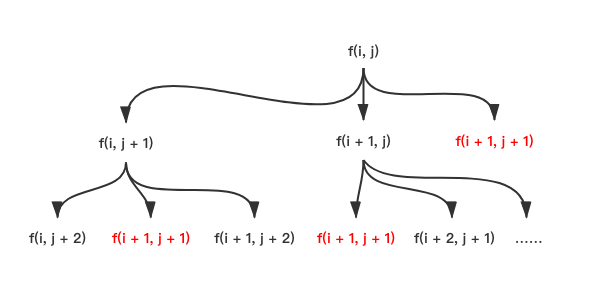
不过仔细观察上图(不仔细也没关系,我给红色高亮了),我们可以发现,为了计算 f(i, j),我们需要计算 f(i + 1, j + 1);而且它也被用于计算 f(i, j + 1) 和 f(i + 1, j) 。
这意味着这个问题存在
重复子问题,类似于我们用 f(i) = f(i - 1) + f(i - 2) 计算
飞波纳妾 fibonacci 数列。
因此我们完全可以将 f(i, j) 存下来、避免重复计算,就像这样:
def change(x, y):
cache = {}
def f(i, j):
if i == len(x):
return len(y) - j
if j == len(y):
return len(x) - i
if (i, j) not in cache:
if x[i] == y[j]:
ans = f(i + 1, j + 1)
else:
ans = 1 + min(
f(i, j + 1),
f(i + 1, j),
f(i + 1, j + 1)
)
cache[(i, j)] = ans
return cache[(i, j)]
return f(0, 0)
注:实际上这里也可以直接用一个二维数组 f[i][j] 来保存 f(i, j),对 C/C++ 来说实现会更容易,读写效率也更高。
优化以后,因为每个 f(i, j) 只需要计算 1 次、并且可以在常数时间里完成(因为子问题已经计算好了),我们将时间复杂度降到了 O(m * n) ,从而可以在短时间内计算出结果了。
- 9 -在这个问题里,还有一个很重要的特性是,我们在计算 f(i, j) 的时候,并不关心从 f(0, 0) 到 f(i, j) 的推导过程,或者说从 f(0, 0) 推导到 f(i, j) 的过程对后续计算 f(i, j) 没有任何影响。用不说人话的方式,这就叫做
无后效性。
注意,无后效性并不是对所有问题都成立的。
比如在一个 N * N 的迷宫里寻找从坐标 (1, 1) 走到 (N, N) 的一条路径,我们在使用 BFS 或 DFS 搜索时需要将路过的坐标做好标记,避免再次走到,因此从 (1, 1) 到 (x, y) 的路径是会影响从 (x, y) 到 (N, N) 的路径,不满足无后效性。
汇总一下前面提到的这个问题的几个特点:
* 最优子结构
* 重复子问题
* 无后效性
—— 这不就是标准的
动态规划 问题嘛!对应的,第 5 节我们推导出的公式,就是这个动态规划问题的
状态转移方程了!

由于满足这几个特性,我们实际上可用迭代的方式,从 f(m, n) 倒推出 f(0, 0),这样可以使用循环而不是递归,进一步提高代码的运行效率。
另外,对于同一个动态规划问题,状态转移方程也可以不止有一种写法,比如我们可以定义 g(i, j) 为将 X[1..i] 变为 Y[1..j] 的最小操作次数,于是:
if X[i] == Y[j]:
g(i, j) = g(i - 1, j - 1)
else:
g(i, j) = 1 + min(
g(i, j - 1),
g(i - 1, j),
g(i + 1, j + 1)
)
基于这一版状态转移方程,我们就可以从 f(0, 0) 开始逐步计算出 f(m, n)。
具体代码就不在这里贴了,感兴趣的同学可以自己写写看,注意边界值的处理就好。
实际上,这个算法叫做
编辑距离,英文名 Levenshtein distance,是一个和普京同名、姓 Levenshtein 的战斗民族大佬在 1965 年提出的算法;该算法经典到 php 的标准库里竟然包含了一个 levenshtein 函数(
可见php的作者真是太闲了)。
- a -还没完,在追求性能和效果的路上我们还能走得更远,根据代码本身的特性,我们还有一些优化可以做。
比如说代码的注释是可以先删掉再比较。
比如说代码里的字符串也可以删掉再比较。
比如说代码里的空格,貌似也不影响我们的相似度对比。
通过这样的操作,我们可以大幅缩短了需要对比的代码长度,对于 O(m*n) 的算法而言,这个改善是很可观的。
此外,当时下场切瓜的另一位瓜友将这个思路推到了极致:既然我们认为代码的整体框架不变、改变的只是变量名这些东西,那我们直接把所有字母、数字、空格等字符全删除,只留下标点符号来代表代码的框架,不是更香吗?
这样我们既提升了计算的效率,又进一步提升了计算的效果。
值得一提的是,该瓜友用的不是编辑距离,而是另一个经典的动态规划算法“最长公共子序列(LCS)”。
- b -啰嗦了这么多,终于可以写总结了:
* 计算两个文本的相似度,可以使用编辑距离或者最长公共子序列算法;这两个都是典型的动态规划算法;
* 动态规划问题需要满足最优子结构、重复子问题、无后效性;
* 要解决动态规划问题,先定义状态,推导状态转义方程,再编码;可以用递归也可以用迭代,前者实现简单,后者运行更快;
* 搞事情要考虑后果,本不应该把参赛账号名也直接公开,结果是那次比赛有些人面子上有点不好看;不过年轻时谁没犯点错呢,除了自己谁又还记得呢?
最后,“编辑距离” 是个 LeetCode 的原题(No. 72,
传送门),;“最长公共子序列” 也是个 LeetCode 的原题(No. 1143,
传送门),感兴趣的同学也别错过。
都看到这儿了,帮忙点个 “赞” 或分享给你的小伙伴吧,感谢~
---
推荐阅读:*
程序员面试指北:面试官视角*
又是面试题?对,合并有序序列。*
踩坑记:go服务内存暴涨*
TCP:学得越多越不懂*
UTF-8:一些好像没什么用的冷知识*
(译) C程序员该知道的内存知识 (1)