Manacher's ALGORITHM: O(n) algorithm for Longest Palindromic Substring
Originated from:
http://blog.csdn.net/ggggiqnypgjg/article/details/6645824
http://zhuhongcheng.wordpress.com/2009/08/02/a-simple-linear-time-algorithm-for-finding-longest-palindrome-sub-string/
中文版
After reading articles listed above and 3 days' thinking, I finally got the idea. In order to save time after forgetting, I decided to record the thoughts here.
First, a clever method is applied to the string to convert all possible LPS to odd-length ones ---- by adding a special char for each gap between chars. For instance, "abba" is transformed to "#a#b#b#a#", and "aba" to "#a#b#a#". To make it simpler, another special char is prepended to the string, thus avoiding extra trival codes to deal with boundary, for example, "$#a#b#b#a#". NOTICE: the code below is written in C, which requires an extra '\0' at the end of a "string"; if you're using another language like python/php, I suggest you add another special char at the end, otherwise you may get over the boundary.
Below I'll explain with "12212321", which in the previous step, is transformed to S = "$#1#2#2#1#2#3#2#1#".
Then I'll use P[i] to record the width (half the length including S[i]) of the Palindromic Substring(PS) which takes S[i] as its center. The relation is shown below:
Now the problem is ---- how to compute P[i]? If we use two extra variables id and mx, where id represents the center of the currently known palindrome sub-string which has the rightmost boundary, and mx represents id + P[id], i.e. the right boundary of that sub-string, then we get to the key point of this algorithm:
If mx > i, then P[i] >= MIN(P[2 * id - i], mx - i).
It looks confusing, and I was stuck at this very point for a long time. But if we unfold the formula, we can get much better understanding:
The code may not be clear enough, but with graphs we can do better.
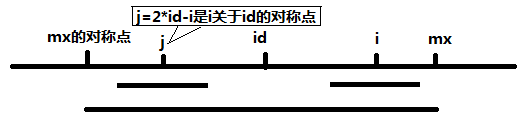
When mx - i > p[j], PS(center=S[j]) is contained by PS(center=S[id]), since the symmetry of i and j, obviously PS(center=S[i]) will be contained by PS(center=S[id]) as well, therefore P[i] = P[j].
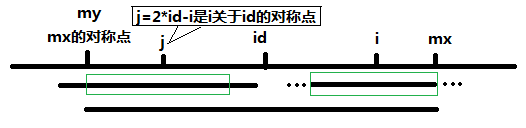
And when P[j] >= mx - i, PS(center=S[j]) is partially contained by PS(center=S[id]), we can assume that at least segments in green boxes (below in the graph) will be the same according to symmetry, which means that PS(center=S[i]) will extend rightwards at least to mx, i.e. P[i] >= mx - i. As for more to the right, we have no choice but to compare forwards char by char.
For cases when mx <= i, we can make no assumption, so, just let P[i] = 1, and compare forwards char by char.
OK, here's the key code:
OVER.
#UPDATE@2013-08-21 14:27
as @zhengyuee pointed out that, since P[id] = mx, therefore S[id-mx] != S[id+mx]. Then, when P[j] > mx - i, we can be sure that P[i] will be just mx - i and no larger. However, neglecting this in practise will only result in an extra comparision (which will definitely fail), while an extra branch have to be added to the code as well, so just neglecting it is fine :)
http://blog.csdn.net/ggggiqnypgjg/article/details/6645824
http://zhuhongcheng.wordpress.com/2009/08/02/a-simple-linear-time-algorithm-for-finding-longest-palindrome-sub-string/
中文版
After reading articles listed above and 3 days' thinking, I finally got the idea. In order to save time after forgetting, I decided to record the thoughts here.
First, a clever method is applied to the string to convert all possible LPS to odd-length ones ---- by adding a special char for each gap between chars. For instance, "abba" is transformed to "#a#b#b#a#", and "aba" to "#a#b#a#". To make it simpler, another special char is prepended to the string, thus avoiding extra trival codes to deal with boundary, for example, "$#a#b#b#a#". NOTICE: the code below is written in C, which requires an extra '\0' at the end of a "string"; if you're using another language like python/php, I suggest you add another special char at the end, otherwise you may get over the boundary.
Below I'll explain with "12212321", which in the previous step, is transformed to S = "$#1#2#2#1#2#3#2#1#".
Then I'll use P[i] to record the width (half the length including S[i]) of the Palindromic Substring(PS) which takes S[i] as its center. The relation is shown below:
S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. You can see that P[i] - 1 is actually the length of the original PS)
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1
(p.s. You can see that P[i] - 1 is actually the length of the original PS)
Now the problem is ---- how to compute P[i]? If we use two extra variables id and mx, where id represents the center of the currently known palindrome sub-string which has the rightmost boundary, and mx represents id + P[id], i.e. the right boundary of that sub-string, then we get to the key point of this algorithm:
If mx > i, then P[i] >= MIN(P[2 * id - i], mx - i).
It looks confusing, and I was stuck at this very point for a long time. But if we unfold the formula, we can get much better understanding:
//let j = 2 * id - i, i.e. the symmetric point of i referring to id
if (mx - i > P[j])
P[i] = P[j];
else /* P[j] >= mx - i */
P[i] = mx - i; //since P[i] >= mx - i, we have to match afterwards since here.
if (mx - i > P[j])
P[i] = P[j];
else /* P[j] >= mx - i */
P[i] = mx - i; //since P[i] >= mx - i, we have to match afterwards since here.
The code may not be clear enough, but with graphs we can do better.
When mx - i > p[j], PS(center=S[j]) is contained by PS(center=S[id]), since the symmetry of i and j, obviously PS(center=S[i]) will be contained by PS(center=S[id]) as well, therefore P[i] = P[j].
And when P[j] >= mx - i, PS(center=S[j]) is partially contained by PS(center=S[id]), we can assume that at least segments in green boxes (below in the graph) will be the same according to symmetry, which means that PS(center=S[i]) will extend rightwards at least to mx, i.e. P[i] >= mx - i. As for more to the right, we have no choice but to compare forwards char by char.
For cases when mx <= i, we can make no assumption, so, just let P[i] = 1, and compare forwards char by char.
OK, here's the key code:
//Input and transform to s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
}
//find the max P[i]
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
}
//find the max P[i]
OVER.
#UPDATE@2013-08-21 14:27
as @zhengyuee pointed out that, since P[id] = mx, therefore S[id-mx] != S[id+mx]. Then, when P[j] > mx - i, we can be sure that P[i] will be just mx - i and no larger. However, neglecting this in practise will only result in an extra comparision (which will definitely fail), while an extra branch have to be added to the code as well, so just neglecting it is fine :)